HW1

Section 1

1.4

1. Suppose that $A\subset B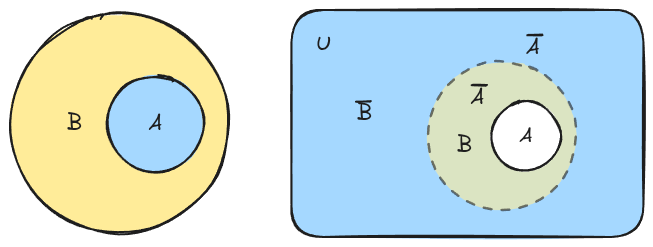$. Show that $B^C\subset A^C$ As shown, $A^C$ includes everything except $A$, which is fully contained inside $B$, and thus $B^C\subset A^C$

7. Suppose that a number $x$ is to be selected from the real line $S$, and let $A,B,C$ be the events represented by the following subsets of $S$:

$$\begin{array}{rl}A& =\{x:1\le x\le 5\},\\ B& =\{x:3<x\le 7\},\\ C& =\{x:x\le 0\}.\end{array}$$

Describe each of the following events as a set of real numbers:

$$\begin{array}{rl}\text{a.}& A^c\\ \text{b.}& A\cup B\\ \text{c.}& B\cap C^c\\ \text{d.}& A^c\cap B^c\cap C^c\\ \text{e.}& (A\cup B)\cap C\end{array}$$ $$A^C=\{x:x>5\vee x<1\}$$ $$A\cup B=\{x:3<x\le 5\}$$ $$B\cap C^C=\{x:3<x\le 7\}$$ $$A^c\cap B^c\cap C^c=\overline{A\cup B\cup C}=\overline{\varnothing }=\mathbb{U}$$ $$(A\cup B)\cap C=\overline{\varnothing }=\mathbb{U}$$

3. A simplified model of the human blood-type system has four blood types: A, B, AB, and O. There are two antigens, anti-A and anti-B, that react with a person’s blood in different ways depending on the blood type. Anti-A reacts with blood types A and AB, but not with B and O. Anti-B reacts with blood types B and AB, but not with A and O. Suppose that a person’s blood is sampled and tested with the two antigens. Let A be the event that the blood reacts with anti-A, and let B be the event that it reacts with anti-B. Classify the person’s blood type using the events A, B, and their complements.

	Anti-A	Anti-B
A	R	NR
B	NR	R
AB	R	R
O	NR	NR

$$A=\{b:B\wedge \neg A\}$$ $$B=\{b:A\wedge \neg B\}$$ $$AB=\{b:\neg A\wedge \neg B\}$$ $$O=\{b:A\wedge B\}$$

1.5

4. If the probability that student A will fail a certain statistics examination is 0.5, the probability that student B will fail the examination is 0.2, and the probability that both student A and student B will fail the examination is 0.1, what is the probability that at least one of these two students will fail the examination?

$$Pr(B\cup A)-Pr(A\cap B)=0.6$$

5. For the conditions of Exercise 4, what is the probability that neither student A nor student B will fail the examination?

$$Pr(\neg A\wedge \neg B)=1-Pr(A\cup B)=0.4$$

6. For the conditions of Exercise 4, what is the probability that exactly one of the two students will fail the examination?

$$Pr(B\cup A)-2Pr(A\cap B)=0.5$$

7. Consider two events A and B with Pr(A) = 0.4 and Pr(B) = 0.7. Determine the maximum and minimum possible values of Pr(A ∩ B) and the conditions under which each of these values is attained.

A and B cannot be disjoint, because $Pr(A)+Pr(B)>1$, so the minimum intersection probability is $Pr(A)+Pr(B)-1=0.1$. The maximum intersection probability is when $A\subset B$, and it’s value is the same as the smaller of the two: $Pr(A)=0.4$.

9. Prove that for every two events A and B, the probability that exactly one of the two events will occur is given by the expression:

$$Pr(A)+Pr(B)-2Pr(A\cap B)$$

In the case that A and B are disjoint, the expression is accurate because the term representing the intersection ($2Pr(A\cap B)$) is equal to zero. Since there is no case where both A and B occur, all cases where either occur are cases where only one occur.

$$\begin{array}{rl}& \forall A,B,(A\cap B=\varnothing ):\\ & \therefore 2Pr(A\cap B)=0\to Pr(A)+Pr(B)-2Pr(A\cap B)=Pr(A)+Pr(B)\\ & \therefore Pr(A)+Pr(B)=Pr(A\cup B)=Pr((A\Delta B)\cup (B\Delta A))\end{array}$$

In the case that A and B are not disjoint, the intersection of A and B is a subset of A and a subset of B. As a result, the probability of only A is the probability of A less the intersection (and likewise for B). Since (only A) and (only B) are by definition disjoint, the probability of one but not both of them is the sum of their individual probabilities. Substituting gives the expression in question.

$$\begin{array}{rl}& (A\cap B)\subset A,(A\cap B)\subset B\\ & Pr(\text{only }A)=Pr(A\setminus (A\cap B))=Pr(A)-Pr(A\cap B)\\ & Pr(\text{only }B)=Pr(B\setminus (A\cap B))=Pr(B)-Pr(A\cap B)\\ & Pr(\text{only one of }A,B)=Pr(\text{only }A)+Pr(\text{only }B)\\ & \therefore Pr(\text{only one of }A,B)=Pr(A)+Pr(B)-2Pr(A\cap B)\end{array}$$

This one also works if A and B are disjoint ($A\cap B=\varnothing$)

11. A point $(x,y)$ is to be selected from the square $S$ containing all points $(x,y)$ such that $0\le x\le 1,0\le y\le 1$. Suppose that the probability that the selected point will belong to each specified subset of $S$ is equal to the area of that subset. Find the probability of each of the following subsets:

(a) the subset of points such that $(x-0.5{)}^2+(y-0.5{)}^2\ge 0.25$

$$A=1-\pi 0.5^2=0.214$$

(b) the subset of points such that $0.5<x+y<\frac{3}{2}$

The two excluded triangles sum to $0.5^2$…

$$A=1-0.5^2=0.75$$

(c) the subset of points such that $y\le 1-x^2$

$$A={\int }_0^1\left(1-x^2\right)dx=\frac{2}{3}$$

(d) the subset of points such that $x=y$ A line has no area, so $Pr(..)=0$