A very long pipe has a distributed charge within it’s volume as ρ(r)=Dar5 where D is a constant, a is the inner, and b is the outer radii.
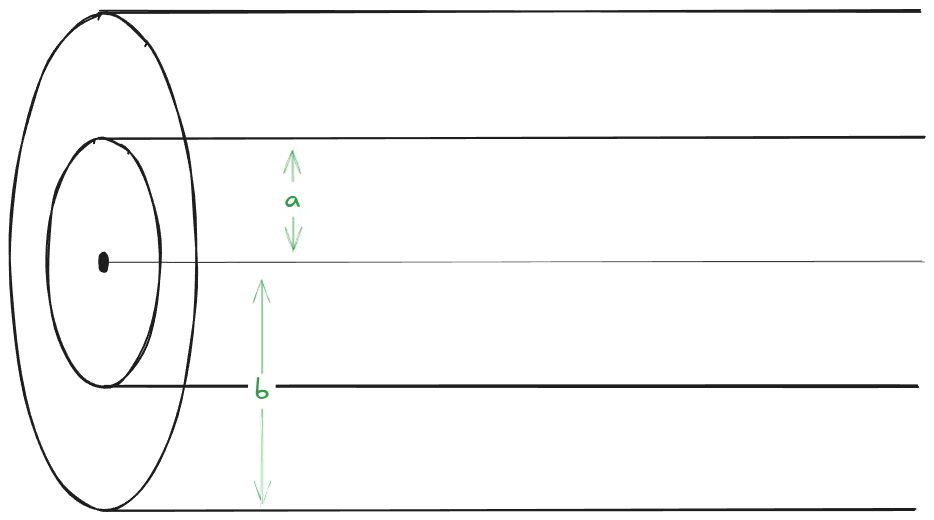
for a<R<b
ϕenc=4πkQenc
Qenc(r)=∫aR2πrlDar5dr
Qenc(r)=a52πlD∫aRr4dr
Qenc(r)=7a52πlD(R7−a7)
E(r)=r1l2k7a52πlD(R7−a7)
E(r)=r2k7a52πvD(R7−a7)
for R>b
E(r)=r2k7a52πvD(b7−a7)
Point charge in solid spherical shell
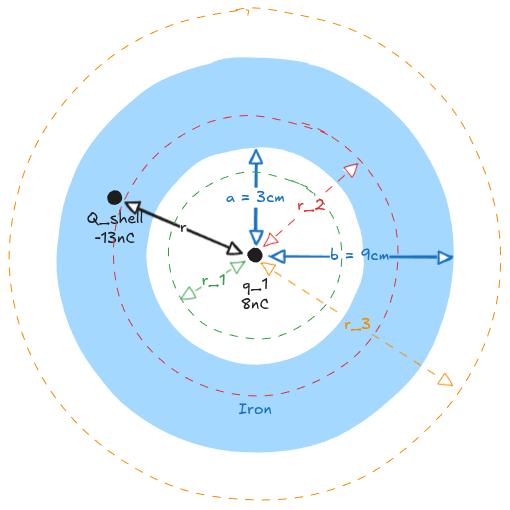
Find E(r1) for r1=2cm
E(r1)=r12kQenc
E(r1)=48.9875⋅109⋅8⋅10−9
E(r1)=48.9875⋅8=17.975
Find E(r2) for r2=4cm
E(r2)=0 for 3cm<r2<9cm
When charges are static, there can be no electric field inside a conductor.
Find E(r3) for r3=11cm
E(r3)=r32kQenc
E(r3)=1128.9875⋅109⋅−5⋅10−9
Er3=−0.371384297521
Calculate the surface charge density on the inner and outer surface of the iron shell
Due to the central charge, Qinner=−8nC;Qouter=8nC
The additional −13nC, will drift to the outer surface, giving:
Qinner=−8nC;Qouter=−5nC
Σinner=4π0.09−8⋅10−9;Σouter=4π0.81−5⋅10−9
Rod in Pipe
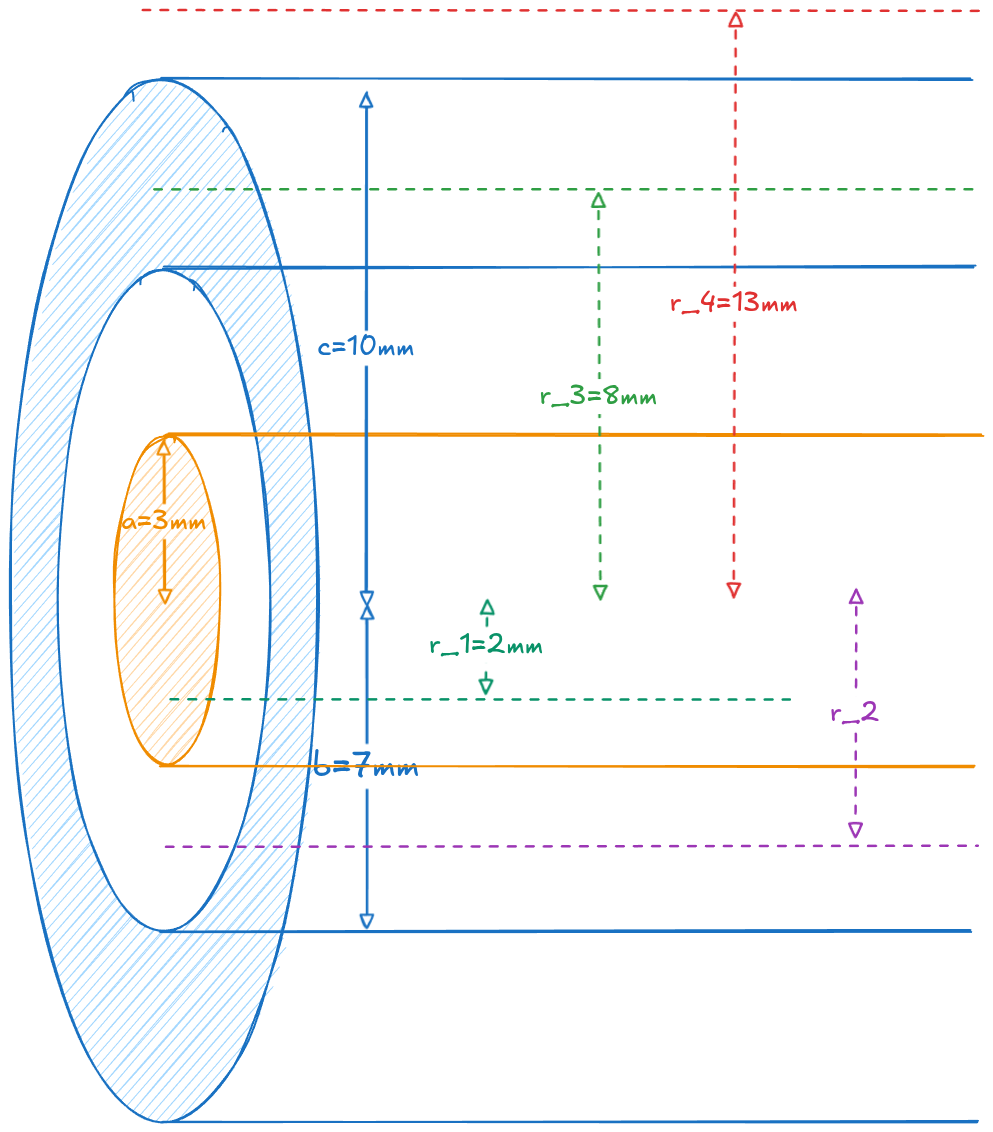
Varied charge over volume sphere
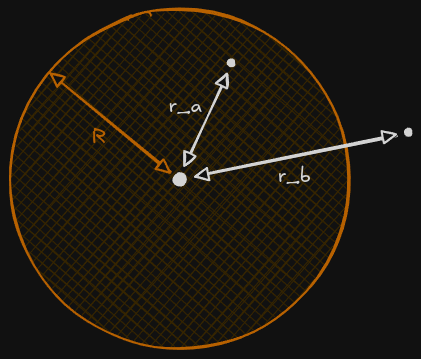
ρ=ar2 for r<R
What is the electric field when r>R?
E=4πra2ϵ0qenc
qenc=∫0R4πr2⋅ar2dr
qenc=4πa ∣0R5r5
E=4πra2ϵ04πa ∣0R5r5
E=ra2ϵ0a ⋅5R5



